티스토리 뷰
작년에 배운 경험이 있으나, 깊이있게 해보지 않고
겉핥기식으로 각 자료구조의 코드 구현 - 백준으로 PS만 대강해보며 넘겼었다.
곧 개강후 전공으로 C로하는 자료구조가 있기에 이번 기회에 윤성우의 열혈 자료구조 책을 참조해 제대로 다져보고자 한다.
(앞으로의 그림 자료들 역시 이 책을 참조하였다)
https://search.shopping.naver.com/book/catalog/32441031922
윤성우의 열혈 자료구조 : 네이버 도서
네이버 도서 상세정보를 제공합니다.
search.shopping.naver.com
1. 알고리즘 성능 평가요소
1. 시간 복잡도(Time Complexity): 얼마나 빠르게 결과를 출력 하는가?, 연산횟수는 얼마나 되는가?
2. 공간 복잡도(Space Complexity): 메모리를 얼마나 사용하는가?
알고리즘 평가시에는 메모리 사용량보다 실행속도에 초점을 두며 중요한 요소로 판단함
=> 중요한 건 시간 복잡도(Time Complexity)

위 그래프에서 데이터 수가 n보다 많다면 A를 선택하는게 일반적
n보다 작을때는 그렇게 중요하지 않다.(어차피 수행속도 비슷함)
2. 점근적 표기법(asymptotic notation)
컴퓨터 알고리즘의 실행시간은 다양한 변수(ex 하드웨어, 운영체제...)로부터 영향을 받기에 100%정확히 측정불가
또한 함수가 복잡해질수록 알고리즘의 효율성을 판단하기 어려워짐
점근적 표기법: 함수를 단순화하여 입력크기 n이 무한대로 커질때
다른 어떤 함수로 근사되는지 간단히 표기하는 방법으로
알고리즘의 수행시간을 표기하기위해 필수적인 부분에 집중하고, 불필요한 부분들은 무시
이러한 점근적 표기법은 3종류가 있고 가장 많이 사용하고 집중적으로 볼 것은 빅오 표기법이다.
빅오 표기법
빅오메가 표기법
빅세타 표기법
빅오 표기법(Big O: O) - 알고리즘(성능)이 최악일때의 실행시간 표기법, 가장 많이 사용하는 분석 방법

위 그래프에서 함수 g(n)을 함수 f(n)의 점근적 상한(asymptotic upper bound)라고 부름.
쉽게 말하면, 주어지는 알고리즘(함수 f(n))이 아무리 나빠도, 비교하는 함수g(n)와 같거나, g(n)보다 빠르다는 것
최악의 관점에서 평가하기에 오히려 가장 정확하다. Why?
상한선을 기준으로 알고리즘을 평가하기에 최악의 경우라 하더라도 효율성이 보장이 된다.
빅오메가 표기법(Ω) - 알고리즘이 최상일때의 실행시간 표기법

위 그래프에서 함수 g(n)을 함수 f(n)의 점근적 상한(asymptotic upper bound)라고 부름.
쉽게 말하면, 주어지는 알고리즘(함수 f(n))이 아무리 좋아도, 비교하는 함수 g(n)와 같거나, g(n)보다 느리다는 것
빅세타 표기법(Θ) - 평균 실행 시간 표기법

위 그래프에서 함수 g(n)을 함수 f(n)의 점근적 상하한(asymptotic tight bound)라고 부름.
f(n)이 g(n)과 거의 동일하다는 것을 뜻하며,
두 함수 f(n)과 g(n)이 빅오 표기법과 빅오메가 표기법에서 모두 참이라면 두 함수는 세타 표기법에 대한 참이 성립한다
빅오메가와 빅오의 교집합이라고 알면 편하다. 다만 평가하기 까다롭다(잘 안씀)
점근적표기법의 3가지에 대해서 배웠지만,,, 제일 중요한건 빅오 표기법이며 이거만 잘 알고 가도 무방
3. 빅오 표기법(Big O: O)
빅오 표기법이란?
함수 f(n)이 있다고 할때, n이 작을때는 무시하며, n이 커질때에 집중한다.
f(n)이 가장 늦게 실행될때(최악)를 상한이라고하며, 빅오표기법은 함수의 상한을 설명한다.
빅오 표기법의 특징?
시간복잡도에 미미한 영향을 주는 요소들을 배제하기에 시간복잡도를 분석하기 쉽다.
아래 3가지 원칙을 따른다.
1. 상수 무시
2. 계수 무시
3. only 최고차항만 표기

빅오 표기법의 종류
| 이름 | 표기법 | 사용하는 자료구조&알고리즘 |
| 상수(Constant)시간 | O(1) | 배열로 원소 접근할때 스택(stack) - push&pop 큐(queue) - enqueue&dequeue 해시테이블(Hashtable)로 원소 접근할때 |
| 로그(logarithmic)시간 | O(logN) | 이진검색(binary search) |
| 선형(linear)시간 | O(N) | 배열에서 검색, 최솟값, 최댓값 찾을때 연결리스트(linked List)에서 순회, 최솟값, 최댓값 찾을때 버킷정렬(bucket sort) 1중 for문 |
| N 로그 N(N log N)시간 | O(NlogN) | 병합정렬(merge sort) 퀵 정렬(quick sort) -평균적 NlogN, 최악은 N^2 힙정렬(heap sort) |
| 이차(quadratic) 시간 | O(N^2) | 버블정렬(bubble sort) 선택정렬(selection sort) 삽입정렬(insertion sort) 2중 for문 |
| 지수(exponential)시간 | O(2^N) | 피보나치 수열(fibonacci numbers) |
| N의 n승(N-Power-n)시간 | O(N^n) | |
| 팩토리얼(factorial) | O(N!) | 팩토리얼(factorial) |
시간복잡도 속도 비교

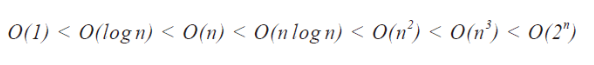
이게 왜 중요할까?
시간복잡도를 파악하지 못한다면, 알고리즘의 문제만 하더라도(ex. 백준이나 실제 코딩테스트 문제)
문제의 요구에 맞게 풀어내기 어렵다.
보통의 알고리즘 문제는 시간 제한 조건으로 2초가 주어진다. 이보다 짧은 1초는 시간복잡도에서 무슨 의미일까?
| 시간복잡도 | 입력 크기 |
| O(1) | 상관X |
| O(logN) | 1억에 근접 |
| O(N) | 1억 |
| O(NlogN) | 500만 |
| O(N^2) | 1만 |
| O(2^N) | 500 |
| O(N^n) | 20 |
| O(N!) | 10 |
코드를 1억번 수행하는데 걸리는 시간이 1초.
전체 수행시간을 어림잡아 시간내에 사용가능한 알고리즘을 생각하고 풀면
문제를 푸는데 더 도움이 된다.(ex. 이 문제는 이 알고리즘을 쓰면 되겟다~)
기타 시간복잡도 - O(NM)
O(NM) - 2중 for문에서 나타날 수 있는 시간복잡도(N^2과 헷갈리지X)
N과 M의 크기가 같다는 보장이 없다면, O(N^2)이 아니라 O(NM)
#include<stdio.h>
int main()
{
int sum = 0;
for(int i = 0;i<5;i++)
{
for(int j = 0;j<3;j++)
{
sum += j;
}
}
printf("%d", sum);
return 0;
}'TIL [자료구조&알고리즘]' 카테고리의 다른 글
| [C] 이중 원형 연결 리스트(DoublyCircularLinkedList) (0) | 2023.03.14 |
|---|---|
| 원형 연결 리스트(CircleLinkedList) (0) | 2023.03.06 |
| 4. 더미노드 있는 연결 리스트(DummyLinkedList) (0) | 2023.03.05 |
| 3. 단일 연결 리스트(SingleLinkedList) (0) | 2023.03.05 |
| 2. 배열 리스트(ArrayList) (0) | 2023.03.02 |
