티스토리 뷰
기존의 배열리스트의 단점
1. 정적인(static) 메모리 구성
배열은 정적인(static) 자료구조로 한번 크기를 정하면 크기 수정이 불가하고
이미 정한 배열 크기 이상의 데이터 개수는 삽입 불가함
2. 배열에 속한 데이터를 삭제하거나, 새로운 데이터 추가시 한칸씩 이동 시켜줘야하는 번거로움
물론 배열리스트와 연결리스트가 시간복잡도면에서 어느 하나가 절대적으로 유리하다고 할 수는 없다.
각각이 지닌 장단점이 다르기 때문이며
둘의 시간복잡도 비교에 대해서는 다른 포스팅을 통해 다루기로 하고 연결리스트에 집중!
연결 리스트(Linked List)
배열 리스트와 달리 메모리의 동적(dynamic)할당을 기반으로 구현된 리스트
연결리스트의 장점
1. 원할때 필요한 만큼 메모리를 동적할당하여 데이터를 생성하여 사용가능
2. 배열리스트의 장점이었던 순차접근도 가능(가장 처음의 주소값 필요)
연결리스트의 종류
연결리스트는 크게 3가지
1. 단일 연결리스트(Single Linked List)
2. 원형 연결리스트(Circular Linked List)
3. 이중 연결리스트(Doubly Linked List)로 구성되며
먼저 가장 기본적인 단일 연결리스트를 다룬 후
더미노드(Dummy Node)를 이용한 단일 연결리스트,
원형 연결 리스트,
이중 연결 리스트,
이중 원형 연결리스트(Doubly Circular Linked List)까지 정리
오늘 구현할 건 단일 연결 리스트
기본적인 단일 연결리스트는 심플한 구성이기에
main함수에 모두 정의하고 구현
단일 연결 리스트(Single Linked List)
아래는 기본적인 예제로 자연수로만 구성된 단일 연결 리스트
처음이기에 코드를 설명하는 그림을 하나하나 그려놓았고,
다음부터는 이해가 필요한 코드 부분만 그린다.
단일 연결리스트 만들기
1. 노드 구조체 정의


2. 노드 포인터들(head, tail, cur, newNode) 초기화
전역변수에 포인터들을 선언(실제 프로젝트에서는 권장되는방법 X but 자료구조 공부가 목적이므로😀)
주의사항. 포인터는 타입에 관계없이 무조건 주소만 저장하며(값 저장 불가❗️) 8바이트(64bit)다.
Node 구조체 포인터들 - head/tail/cur/newNode
head
첫번째 노드를 가리키며, 연결리스트를 만들때 무조건 필요함.
tail
마지막 노드를 가리키며 어떤 연결리스트를 만드냐에 따라 필요성의 여부가 판단된다.
장점은 tail 포인터는 맨 마지막 노드의 주소를 가리키기 때문에, 맨마지막 삽입시 시간복잡도가 O(1)로 처리 가능하다. (없다면 head포인터부터 끝까지 돌아야함. O(N) 시간복잡도)
cur
순차 접근을 위한 노드로 연결리스트를 만들때 무조건 필요함
newNode
Node구조체 포인터로 동적할당(malloc 함수)을 통해 실제로 생성해 데이터를 저장할 노드


3. ⭐️삽입(추가)⭐️
삽입에는 일반적인 (순행)삽입과 역순삽입이 있음(앞으로도 추가하고, 뒤로도 추가가능)
삽입은 첫노드일 경우와, 2번째 이후의 노드의 경우로 분리해야함
why?
단일연결리스트는 일방 통행과 같다.
head포인터가 맨 첫번째 노드를 가리켜야,
그 첫번째 노드의 주소값으로 시작하여 마지막 노드까지 접근 가능하다.
(물론tail포인터만으로도 데이터 접근은 가능하나 일반적으로 head포인터로 데이터에 접근한다)
1. 순행 삽입
노드 삽입하기
1. 노드를 만들고 데이터를 저장
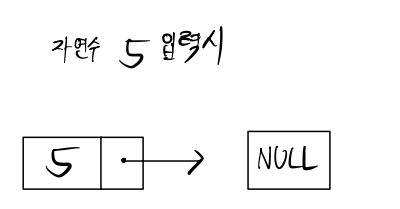
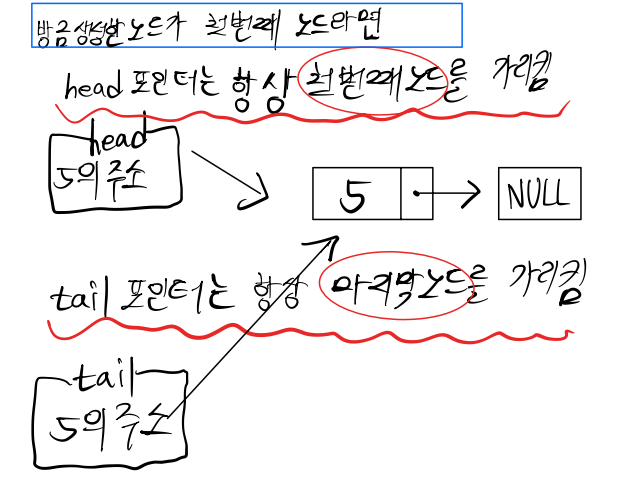
2. 순행 삽입이기에 1번째 삽입한 노드는 head 포인터로 가리켜준다
-> head에 1번째 노드 주소값 저장(값(value)저장 X)
tail 포인터 역시 가리켜준다(순행 삽입이므로 tail포인터를 통해 연결해줘야함)
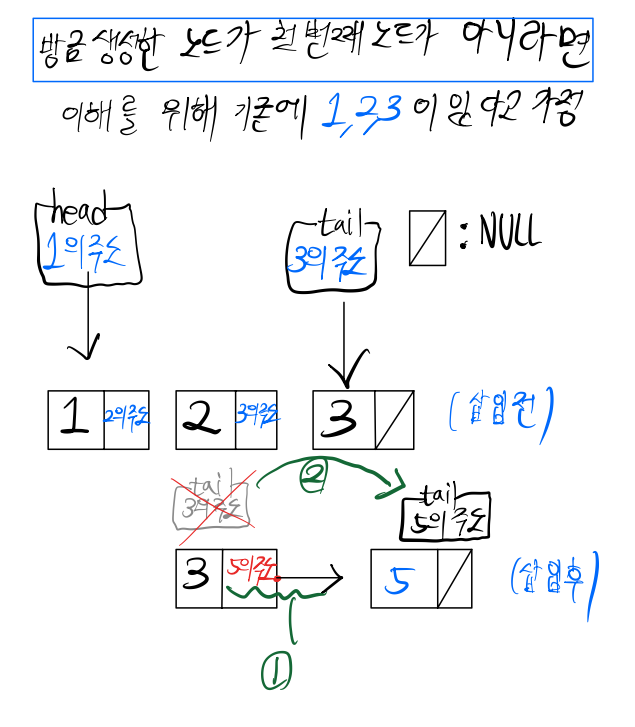
3. 2번째 노드부터 삽입할때에는 tail이 그 이전의 newNode를 가리키고 있기 때문에
tail이 가리키는 노드뒤에 삽입한다.

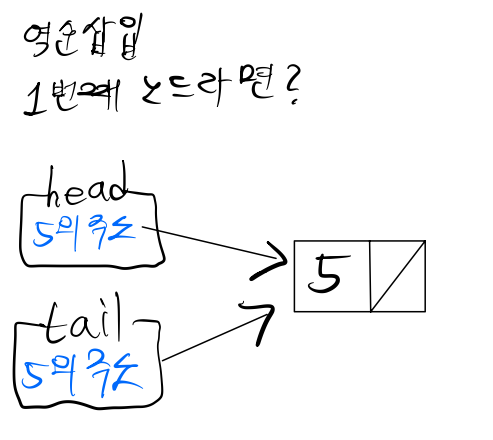
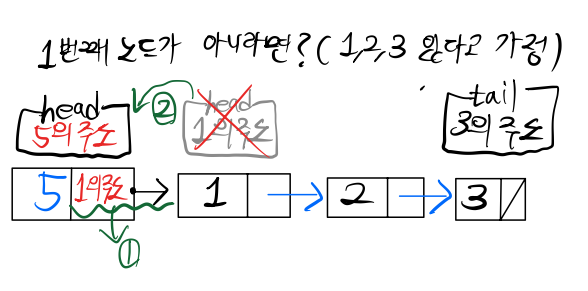
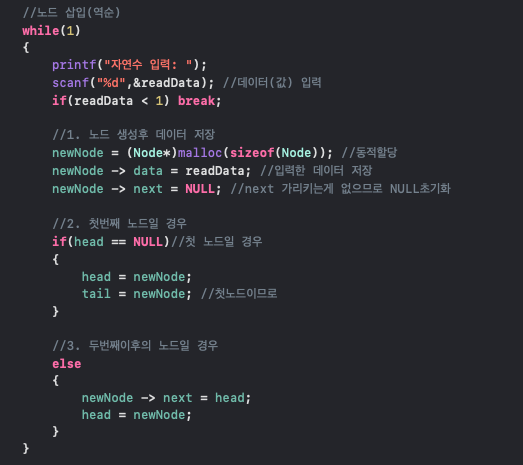
2. 역순삽입
순행삽입은 꼬리(tail)에 데이터를 추가하는 방식이었다면
역순삽입은 head에 데이터를 추가하는 방식
(else문만 다르다)
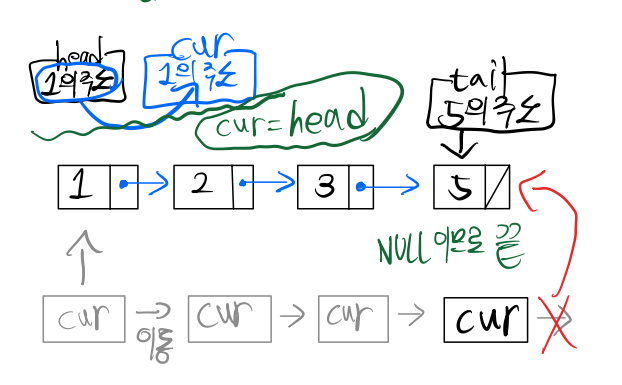
4. 순회: cur노드를 통해 노드 순회하기
while(cur != NULL)은 마지막 노드를 가리키기전까지 계속해서 cur위치를 1칸씩 이동

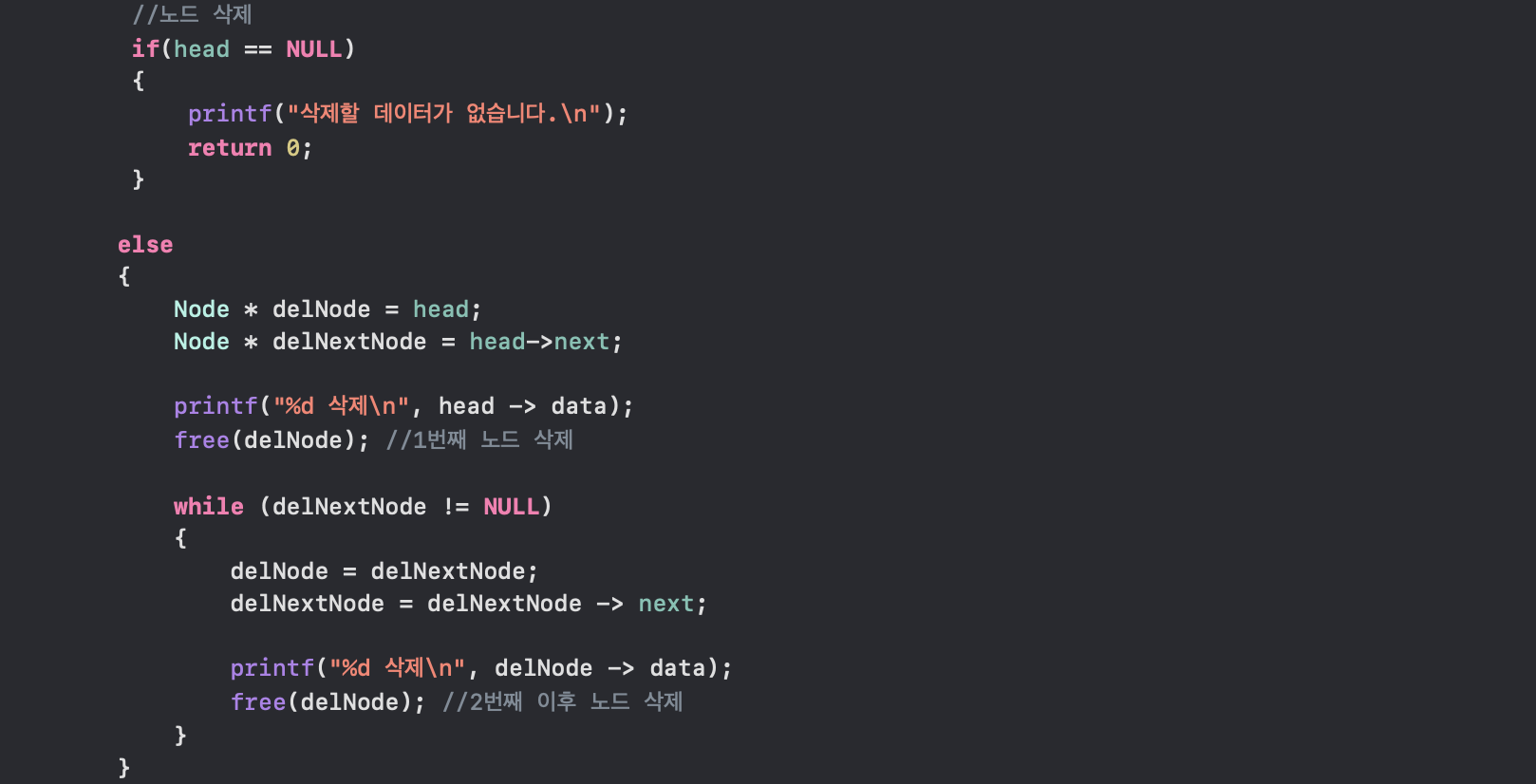
5.삭제: delNode를 생성하여 데이터 삭제(메모리 해제) 시키기
while문은 순회시 cur노드를 이동시키는것과 같은 매커니즘 -> 마지막 노드까지 전부 삭제
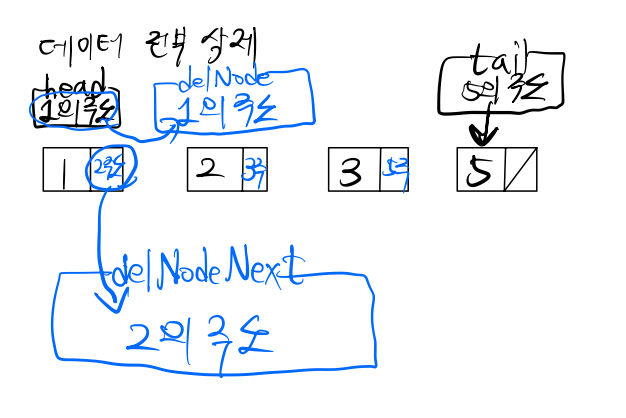
delNode와 delNextNode를 나누는 이유는 head포인터가 가리키는 노드를 그냥 삭제한다면,
그 다음 노드에 접근이 불가하기에 삭제될 노드가 가리킬 다음노드의 주소값을 저장하기 위해
별도로 delNextNode를 생성하여 삭제될 노드의 다음 노드의 주소를 저장해 둠(연결리스트에서 자주 보게 되는 방식)
ex) 윗 그림에서 1이 들어가 있는 노드를 삭제한다면,
다음 데이터인 2의 주소값에 접근할 노드가 필요한데
1의 데이터는 delNode에 담겨있고, free로 메모리에서 해제 되었으므로
delNode로는 접근 불가함 => delNextNode의 필요성(delNextNode에는 2의 주소가 담겨있음)
단일 연결 리스트 코드 전체
#include<stdio.h>
#include<stdlib.h>
typedef struct node{
int data;
struct node* next; //다음 노드를 가리키는 포인터(연결을 담당한다)
}Node;
int main()
{
//가리키는 것이 없다는 뜻으로, 먼저 NULL로 초기화 해준다
Node*head = NULL;
Node*tail = NULL;
Node*curNode = NULL;
Node*newNode = NULL;
int readData;
// 노드 삽입(역순 저장)
// while(1)
// {
// printf("자연수 입력: ");
// scanf("%d",&readData);
// if(readData < 1) break;
//
// newNode = (Node*)malloc(sizeof(Node));
// newNode -> data = readData;
// newNode -> next = NULL;
//
// //1단계
// if(head == NULL)//첫 노드일 경우
// {
// head = newNode;
// tail = newNode;
// }
// else
// {
// newNode -> next = head;
// head = newNode;
// }
// }
//노드삽입(순행 저장)
while (1) {
printf("자연수 입력: ");
scanf("%d",&readData);
if(readData < 1) break;
newNode = (Node*)malloc(sizeof(Node));
newNode -> data = readData;
newNode -> next = NULL;
//1단계
if(head == NULL) head = newNode;
else tail -> next = newNode;
tail = newNode;
}
//노드 조회
if(head == NULL)
printf("저장된 자연수가 없습니다.\n");
curNode = head;
while(curNode != NULL)
{
printf("%d\n", curNode -> data);
curNode = curNode -> next;
}
//노드 삭제
if(head == NULL)
{
printf("삭제할 데이터가 없습니다.\n");
return 0;
}
else
{
Node * delNode = head;
Node * delNextNode = head->next;
printf("%d 삭제\n", head -> data);
free(delNode); //1번째 노드 삭제
while (delNextNode != NULL)
{
delNode = delNextNode;
delNextNode = delNextNode -> next;
printf("%d 삭제\n", delNode -> data);
free(delNode); //2번째 이후 노드 삭제
}
}
return 0;
}
'TIL [자료구조&알고리즘]' 카테고리의 다른 글
| [C] 이중 원형 연결 리스트(DoublyCircularLinkedList) (0) | 2023.03.14 |
|---|---|
| 원형 연결 리스트(CircleLinkedList) (0) | 2023.03.06 |
| 4. 더미노드 있는 연결 리스트(DummyLinkedList) (0) | 2023.03.05 |
| 2. 배열 리스트(ArrayList) (0) | 2023.03.02 |
| 1. 알고리즘 성능 분석 수단(Time Complexity, Big O) (0) | 2023.02.28 |
